
CROSS ENTROPY LOSS FUNCTION CODE
We have already had a code to create data that consists of two Gaussian clouds, one of which has a center point (-2 -2), and the second one has a point (+2 +2). The only difference is that we also import the Matplotlib library this time. We copy the code from the previous article. In this section of the article, we graphically depict the solution for the Bayes classifier, which we have found above. If you run the program, you can make sure that the cross-entropy error becomes significantly less when we use a particular solution of logistic regression. We recommend you to calculate by yourself that the offset is zero, and both weighting factors are 4, to understand where such figures exactly come from. Its use is legitimate since our data have the same variance in both classes. It would be nice to find an already considered private solution for logistic regression. It depends on the value of the target variable and the output variable of the logistic regression. Now write a function for computing the cross-entropy error function. We can also copy the creation of a column of ones from the previous code, as well as the part of the code devoted to calculating the sigmoid. The first 50 ones belong to class 0, and the other 50 ones are in class 1. Let’s create an array of target variables. Now we create two of our classes, so that the first 50 points are concentrated in the zone with the center (-2 -2), and the second 50 ones are in the zone with the center (+2 +2). Now let`s examine the calculation of the cross-entropy error function in the code.įirst, we transfer a part of the code from the previous file. Thus, we have a common cross-entropy error function: To do this, we summarize the values of all the individual errors from 1 to N. Thus, the cross-entropy error function works as we have expected.įinally, note that we need to calculate a common error to optimize the model parameters across the data set simultaneously. As a result, we get 2,3 as the value of error function that is even more important. Now let t = 0, y = 0,1, so we are very much mistaken. This is a serious error that indicates that the model doesn`t work properly. If we set t = 1, y = 0.5, so the model is on the verge of correctness, then we get 0.69 as a result of the error function. It is a minimal error, so everything is also wonderful here.
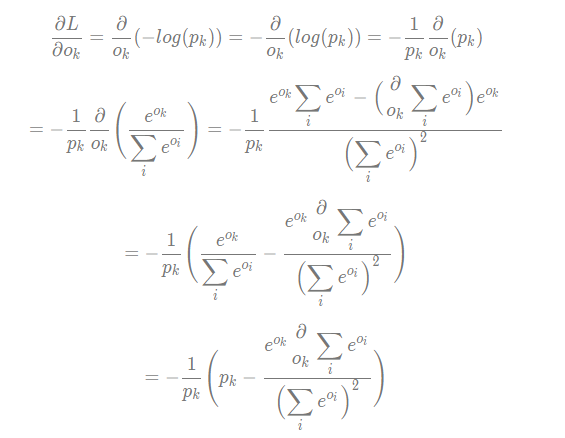
Now let t = 1, y = 0.9, so the model is almost correct. Note that if t = 0, y = 0, then we have the same result. As a result, we get one multiplied by zero, that is zero.
CROSS ENTROPY LOSS FUNCTION PLUS
Thus, having received minus infinity, we will get plus infinity as a result. But pay attention to the minus sign in the formula. Since y is the output variable of logistic regression that takes a value from zero to one, the logarithm of this quantity takes values from zero to minus infinity. If t = 1, the first term is significant, if t = 0, then the second term is significant. This is because the target variable t takes values only 0 and 1. Where t is a target variable, y is a result of logistic regression.įirst of all, we note that only one term of the equation is essential. The cross-entropy error function is defined as follows: So, let’s see how the cross-entropy function does it all.
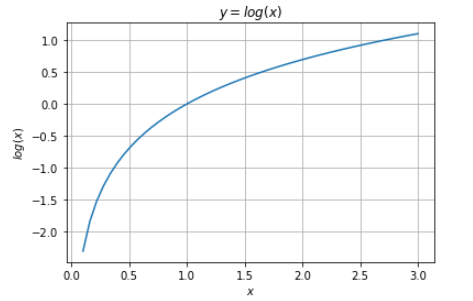
That’s why we need another error function.įirst of all, it should equal zero if there are no errors, and have a larger value if lots of errors appear. Of course, the error cannot have the Gaussian distribution with logistic regression, since the result is between zero and one, and the target variable takes values only 0 and 1. Given what we know about the color of the points, how can we evaluate how good (or bad) are the predicted probabilities? This is the whole purpose of the loss function! It should return high values for bad predictions and low values for good predictions.įor a binary classification like our example, the typical loss function is the binary cross-entropy / log loss. If we fit a model to perform this classification, it will predict a probability of being green to each one of our points. In this setting, green points belong to the positive class ( YES, they are green), while red points belong to the negative class ( NO, they are not green). Since this is a binary classification, we can also pose this problem as: “ is the point green” or, even better, “ what is the probability of the point being green”? Ideally, green points would have a probability of 1.0 (of being green), while red points would have a probability of 0.0 (of being green). So, our classification problem is quite straightforward: given our feature x, we need to predict its label: red or green.


 0 kommentar(er)
0 kommentar(er)
